想要解好数学题，我们首先要搞清楚：数学，有什么用？
咱们眼下最重要的事情，当然是考试拿分。所以，这个问题的回答，我们将讨论范围，限制到中高考范围内。如果想了解得更深入，请多参考专业人士的回答。
数学，最早是为了解决具体问题，比如让某个祖先搞清楚自己有多少粮食，几个孩子……所以，相关知识点，肯定指向具体的事物。比如1.2.3.4.5，很有可能是从树上发明出来的。无非是后期研究的东西复杂了点儿，为了方便研究，就发明了些简化的符号。就好像证明题里的三角形，在实际生活中，可能是指谁家的粮仓，甚至金字塔。
总结一下：知识点，描述具体事物。
那么，某个数学题不明白的话，处理方案也就出来了：回归到他所描述的事物。搞清楚那些东西有什么特点，有时候，问题就解决一大半了。
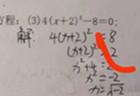
比如这个错题，做题人显然认错了题干上的知识点：人家是个完全平方式，他却硬要往同底数幂的公式上套。结果本来开个根号就完事儿了，拖那么几行，最后还错了。这就是典型的：手里有把锤子，就看什么就像钉子。
再比如上面这两个，也是相同的问题。题上，明明是立方根，非要按平方根的解法来。81身上披了个那么大的根号，就是看不见。
为什么会这样？因为，没有安心搞清楚题目涉及的内容的特点（本质）。把老师们总结的快捷方式（公式技巧），当成了灵丹妙药。他们对题目一点都不真诚，他们又怎么可能帮咱们拿分呢？
精确，是数学跟其他科目相比，最大的特点。他不光表现在数字上，也表现在相关内容的内涵上。而后者，才是中高考数学的重点。
复习下我们暑假最后一课：
无论多难的题目，都可以拆解成不同的小环节。我们对这些环节的理解越清楚深入，就越能找到不同环节之间的连接方式，从而确定主要矛盾。搞定了他，剩下的都是体力活。
本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请发送邮件至 3231169@qq.com 举报，一经查实，本站将立刻删除。
如若转载，请注明出处：https://www.kuaisuzugao.com/1254.html
如若转载，请注明出处：https://www.kuaisuzugao.com/1254.html
